试题详情
简答题 圆周角定理证明思路如下：将圆周角的两边所处的位置分成三种情况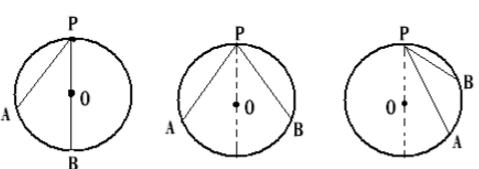： ①角的一边落在直径上； ②角的两边在某一直径的两侧； ③角的两边在某一直径的同侧。 如图所示。先对情况①进行证明，然后将情况②、③转化为情况①分别进行证明。最后得出圆周角定理对任意圆周角都成立的结论。 试具体分析上述证明中需要用到哪些数学思想方法。
  • 该证明中用到下面几种数学思想方法：
    ①将圆周角分成三种情况，用到分类方法；
    ②先证明角恰有一边在直径上的特殊情况，用到特殊化方法；
    ③将其他两种情况转化为角恰有角恰有一边在直径上的情况，用到化归方法；
    ④通过对所有三种情况的证明，然后得出圆周角定理的结论，用到完全归纳法；
    ⑤在证明过程中需要进行演绎推理，因此用到演绎方法。

  • 关注下方微信公众号，在线模考后查看

热门试题