试题详情
- 简答题已知某离散系统的系统函数为
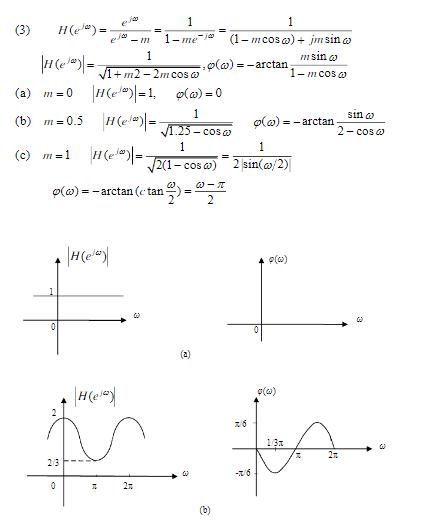
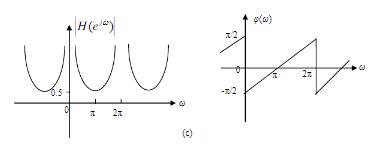
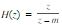,m为常数。 （1）写出对应的差分方程； （2）画出该系统的结构图； （3）求系统的频率响应特性，并画出m = 0,0.5,1三种情况下系统的幅频特性与相频特性曲线。
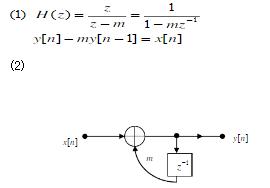
关注下方微信公众号，在线模考后查看
热门试题
- 函数的单边拉普拉斯变换为（），函数的逆变
- 粗略地估计如图所示各脉冲的频带宽度B
- 线性系统响应满足以下规律（）。
- 一线性时不变因果连续时间系统的微分方程描
- 冲激函数的频谱曲线，经过低通滤波器后的波
- 离散时间系统的频率响应是如何定义的？它的
- 已知系统如题图所示，其中输入信号
- 已知f（t）的频带宽度为Δ&
- 写出如图所示各梯形网络的电压转移函数，在
- 系统函数与激励信号无关
- 已知x（t）的傅里叶变换为X（j&ome
- 零输入响应就是由输入信号产生的响应。
- 周期信号 试求该周期信号的基波周期T，
- 绘出下列时间函数的波形图: f
- 周期信号f（t）如题图所示，若重复频率f
- 离散系统函数H（z）的零极点分布如图所示
- 如题图一阶系统，对（a）求冲激响应i和u
- 连续周期信号的频谱具有（）
- 差分方程所描述系统的单位函数响应h（k）
- 一线性时不变离散时间因果系统的直接型模拟