试题详情
- 简答题设二维离散型随机变量（X,Y）只取（0,0）,（-1,1）,（-1,2）及（2,0）四对值，相应概率依次为
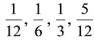，试判断随机变量X与Y是否相互独立。
关注下方微信公众号，在线模考后查看
热门试题
- 设二维随机变量，则（）。
- 证明：对取值于区间（a，b）内的随机变量
- 设平面区域D由曲线y=1/x及直线y=0
- 某车间生产滚珠，其直径X～N（μ，
- 设随机变量X服从（1，6）上的均匀分布，
- 设随机变量X和Y的联合分布为： 验证：
- 已知二维随机变量（X，Y）的联合概率密度
- 对球的直径作近似测量，设其值在区间 [a
- 有2500名同一年龄和同社会阶层的人参
- 设P（A）=0.4，P（A+B）=0.7
- 袋中有12个零件，其中9个合格品，3个废
- 从汽车轮胎厂生产的某种轮胎中抽取10个样
- 设总体α，β未知，
- 设两个随机变量X与Y相互独立且同分布，P
- 游客乘电梯从电视塔底层到电视塔顶层观光
- 电路由电池a与两个并联的电池b及c串联而
- 设总体X~N（μ，σ2
- 测得16个零件的长度（mm）如下： 设
- 已知事件A、B的概率分别为P（A）=0.
- 10件产品中有6件正品，4件次品，对它们