试题详情
- 简答题盒子里装有3只黑球,2只红球,2只白球,在其中任取4只球,以X表示取到黑球的只数,以Y表示取到白球的只数,求X,Y的联合分布律。
-
(X,Y)的可能取值为(i,j),i=0,1,2,3,j=0,12,i+j≥2,联合分布律为
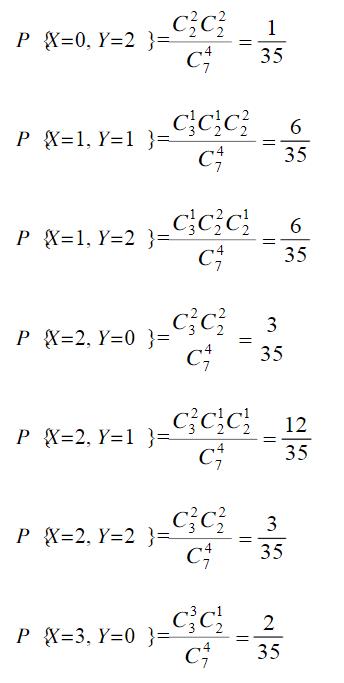
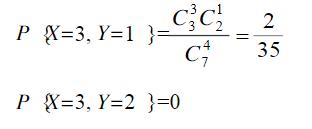
关注下方微信公众号,在线模考后查看

热门试题
- 50个产品中有46个合格品与4个次品,从
- 已知男子有5%是色盲患者,女子有2%是色
- 设A,B为随机事件,且P(A)=0.6,
- 设随机变量(X,Y)概率密度为 求P(
- 已知X-N(-3,1),Y-N(2,1)
- 已知离散型随机变量X的概率分布为:P{X
- 10张奖券中含有3张中奖的奖券,现有三人
- 设总体从总体X中抽取容量为10的样本,从
- 对任意随机变量X,若EX存在,则E[E(
- 设事件A与事件B互不相容,则()
- 设二维离散型随机变量(X,Y)的联合分布
- 盒中有10个合格品,3个次品,从盒中一件
- 设总体X~N(20,3),分别取样本容量
- 以X表示某种小包装糖果的重量(以g计),
- 如图1,2,3,4,5表示继电器接点,假
- X为随机变量,则DX=Cov(X,X)
- 用一种检验法检测产品中是否含有某种杂质的
- 设总体X的密度函数为f(x,&theta
- 在下列条件下,求: 已知P(A)=0.
- 设随机变量X服从泊松分布,且P{X=1}