试题详情
- 简答题画图说明牛顿迭代公式的几何意义。
-
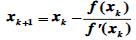
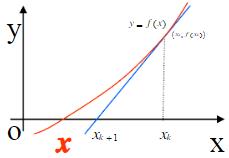
牛顿迭代公式就是切线与 x 轴交点的横坐标,所以牛顿法是用切线与 x 轴的交点的横坐标来近 似代替曲线与x 轴交点的横坐标。
关注下方微信公众号,在线模考后查看

热门试题
- 用Gauss列主元消去法解方程组:。
- 用牛顿(切线)法求的近似值。取x
- 导出中点公式(或称Euler两步公式),
- 试讨论用Jacobi迭代法和Gauss-
- 已知方程x3-x<
- 设,试说明A为可约矩阵。
- Jacobi迭代法解方程组Ax=b的必要
- ,则=(),A的谱半径ρ(A)=
- 在[a,b]上求插值多项式H3
- 用高斯-约当方法求A的逆阵:
- 拉格朗日插值多项式的余项是()
- 试确定常数A,B,C和α,使
- 对一元2次方程具有5位有效数字,求其具有
- 用梯形法解初值问题y′=x2<
- 解初始值问题近似解的梯形公式是y
- 迭代法的收敛条件是(1)(),(2)()
- 3.142和3.141分别作为π的近似数
- 观测物体的直线运动,得出以下数据,求运动
- x*为精确值x的
- 用下列方法计算积分比较结果 (1)龙贝格