试题详情
- 简答题 设
，试说明A为可约矩阵。
-
取排列阵P=I23，则
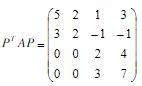
A.为可约矩阵。 关注下方微信公众号，在线模考后查看
热门试题
- 试划出部分选主元素三角分解法框图，并且用
- 设f（x）=x4+
- 设x=（11，0，5，1）T<
- 设A与B为n阶矩阵，A为非奇异，考虑解方
- 设初值问题 a）写出由Euler方法、取
- 利用公式求下列各近似值的误差限： 其中
- 求一个次数小于等于三次多项式p（x），满
- 设，试说明A为可约矩阵。
- 设x∈Rn
- 用梯形方法解初值问题 证明其近似解为
- 设有1计算机：n=3，-L=U=2，&b
- 分别用二阶显式亚当姆斯方法和二阶隐式亚当
- 证明n阶均差有下列性质：若F（x）=cf
- 设 （1）试求f（x）在上的三次Herm
- 设f（x）∈C[a，b]，把[a，b]分
- 设，则ρ（A）为（）。
- 什么是矩阵的条件数？如何判断A是病态的或
- 证明：切比雪夫多项式序列
- 用辛普森公式求积分并计算误差
- 给定迭代过程，x（k+1）