试题详情
- 简答题 用梯形方法解初值问题
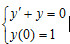证明其近似解为 
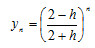并证明当h→0时，它收敛于原初值问题的准确解y=e-x。
-
关注下方微信公众号，在线模考后查看
热门试题
- 下列方程组Ax=b，若分别用J法及GS法
- 有一个长方形水池，由测量知长为（50±0
- 设x1=1.216
- 用1+x近似表示ex
- 欲使线性插值具有4位有效数字。在区间[0
- 设x*是非线性方程
- 用雅可比、高斯-塞德尔迭代法，求解方程组
- 直接验证柯特斯公式具有5次代数精度。
- f（1）=-1，f（2）=2，f（3）=
- 解初值问题的改进欧拉法是（）阶方法。
- 已知常微分方程的初值问题： 用改进的Eu
- 设x∈Rn
- 迭代法的收敛条件是（1）（），（2）（）
- -324.7500是舍入得到的近似值，它
- f（x）是[-a，a]上的连续奇（偶）函
- 给定插值点（xi，
- 用复化梯形公式求积分，问要将积分区间[a
- 设初值问题y′=x
- 设xk=x
- 设x的相对误差为2％，求xn<