试题详情
- 简答题 利用公式求下列各近似值的误差限:
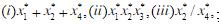 其中
其中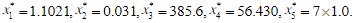
-
如下:
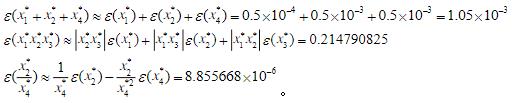
关注下方微信公众号,在线模考后查看

热门试题
- 对初值问题证明用梯形公式所求得的近似值为
- 证明
- 解初值问题的改进欧拉法是()阶方法。
- 用Gauss-Seidel迭代法求解线性
- 导出中点公式(或称Euler两步公式),
- 试讨论用Jacobi迭代法和Gauss-
- 求解方程组的高斯—塞德尔迭代
- 比较求ex+10x
- 对方程组 (1)试建立一种收敛的Sei
- 画图说明牛顿迭代公式的几何意义。
- 设x的相对误差为a%,求y=x
- 构造一个三次多项式H(x),使它满足条件
- 已知用线性插值求的近似值。(拉格朗日线性
- 设x=(1,9,-5,2)T<
- 计算方法主要研究()误差和()误差。
- 用牛顿切线法解方程f(x)=0,选初始值
- 下述矩阵能否分解为LU(其中L为单位下三
- 对f(x)=sinx在[0,π/2]上求
- 取步长h=0.2,求解初值问题,用欧拉预
- 分别描述R2中(画