试题详情
- 简答题 求解方程组
 的高斯—塞德尔迭代格式为(),该迭代格式的迭代矩阵的谱半径ρ(M)=()。
的高斯—塞德尔迭代格式为(),该迭代格式的迭代矩阵的谱半径ρ(M)=()。
-
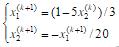 ;
;
关注下方微信公众号,在线模考后查看

热门试题
- 证明对于任意选择的A,序列收敛于零
- 计算球的体积,为了使体积的相对误差限为1
- 利用尤拉公式求解初值问题,其中步长h=0
- 用适当的迭代法求下列方程组的根,精确至4
- 已知用线性插值求的近似值。(拉格朗日线性
- (a)设A是对称矩阵,λ和
- 方程组: 写出用J法及GS法解此方程组的
- 用牛顿法求的近似值,取x0
- 已知y=f(x)的数据如下: 求二次插
- 应用牛顿法于方程f(x)=xn
- 迭代过程xk+1=
- 计算积分,取4位有效数字。用梯形公式计算
- 设xk=x
- 用二分法求方程的正根,要求误差小于0.0
- 设计算机具有4位字长。分别用Gauss消
- 用辛浦生公式计算积分近似值;
- 绘图题:画出SOR迭代法的框图。
- 设A∈Rn×n,求
- 证明等式试依据nsin(π/n)(
- 确定下列公式中的待定参数,使其代数精度尽