试题详情
- 简答题 用牛顿法求
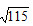的近似值，取x0=10或11为初始值，计算过程保留4位小数。
-
关注下方微信公众号，在线模考后查看
热门试题
- 求证的充要条件是对任何向量x，都有
- 已知x=[0，-1，2]T
- 设f（x）=sinπx.，求f（x）于[
- 用改进的欧拉公式，求以下微分方程 的数
- 已知近似值xA=2
- 解初始值问题近似解的梯形公式是y
- 面Matlab程序所求解的数学问题是（）
- 证明对于任意选择的A，序列收敛于零
- 设A是对称正定矩阵，经过高斯消去法一步后
- 用追赶法求解三对角方程组
- 利用反幂法求矩阵的最接近于6的特征值及对
- 直接验证柯特斯公式具有5次代数精度。
- 构造一个三次多项式H（x），使它满足条件
- 设f（x）∈C2
- 设f（x）∈C[a，b]，把[a，b]分
- 取5个等距节点 ，分别用复化梯
- 试确定常数A，B，C和a，使得数值积分公
- 当N充分大时，怎样求
- 证明迭代公式是计算的三阶方法。假定初值x
- 设A为n阶非奇异矩阵且有分解式A=LU，