试题详情
- 简答题 （a）设A是对称矩阵，λ和
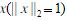是A的一个特征值及相应的特征向量，又设P为一个正交阵，使Px=e1=（1，0，...0）T 证明B=PAPT的第一行和第一列除了λ外其余元素均为零。 （b）对于矩阵 
λ=9是其特征值，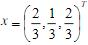
是相应于9的特征向量，试求一初等反射阵P，使Px=e1，并计算B=PAPT。
-
关注下方微信公众号，在线模考后查看
热门试题
- 实数a≠0，考察矩阵，试就方程组A
- 已知求解线性方程组Ax=b的分量迭代格式
- 写出求方程4x=cos（x）+1在区间[
- 若f（x）∈C2
- 对方程组 （1）试建立一种收敛的Sei
- 设初值问题 （1）写出用Euler方法
- 设Lk为指标为k的
- 递推公式，如果取y0
- 计算方法实际计算时，对数据只能取有限位表
- 用二步法求解一阶常微分方程初值问题，问：
- 求一个次数小于等于三次多项式p（x），满
- 用1+x近似表示ex
- 对于给定的线性方程组 （1）讨论雅可比迭
- 用龙贝格方法计算积分，要求误差不超过10
- 根据下列f（x）=tanx的数值表：
- 用带位移的QR方法计算 全部特征值。
- 迭代过程xk+1=
- 设有函数值表：
- 设A∈Rn×n，且
- 设f（x）=x7+