试题详情
- 简答题 设初值问题
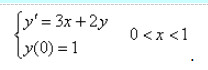（1）写出用Euler方法、步长h=0.1解上述初值问题数值解的公式； （2）写出用改进的Euler法（梯形法）、步长h=0.2解上述初值问题数值解的公式，并求解y1，y2，保留两位小数。
-
关注下方微信公众号，在线模考后查看
热门试题
- 求a，b使为最小。
- 画图说明牛顿迭代公式的几何意义。
- 已知高斯求积公式将区间[0，1]二等分，
- 用二步法求解一阶常微分方程初值问题，问：
- 已知常微分方程的初值问题： 用改进的Eu
- 已知f（1）=1.0，f（2）=1.2，
- 试确定常数A，B，C和a，使得数值积分公
- 有常微分方程的初值问题，试用泰勒展开法，
- 设∥A∥P,∥A∥
- 若f（x）∈C2
- 求矩阵 与特征值4对应的特征向量。
- 用列主元消去法求解方程组 并求出系数矩
- 设 （1）试求f（x）在上的三次Herm
- 已知方程x3-x<
- 设Ux=d，其中U为三角矩阵。 （a）
- 设计一个计算的牛顿迭代法，且不用除法（其
- 已知a=1.2031，b=0.978是经
- 已知： 分别用拉格朗日插值法和牛顿插值
- 如果方阵A有aij
- 在[-1，1]上利用插值极小化求f（x）