试题详情
- 简答题 有常微分方程的初值问题
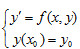，试用泰勒展开法，构造线性两步法数值计算公式
，使其具有二阶精度，并推导其局部截断误差主项。
-
关注下方微信公众号，在线模考后查看
热门试题
- 设A为n阶非奇异矩阵且有分解式A=LU，
- 已知方程组Ax=b，其中 （1）列出J
- 对于初值问题，证明当h<0.2时，欧拉公
- 设空间φ1=spa
- 应用Newton法分别导出求方程
- 用三点公式和五点公式分别求在x=1.0，
- 设x0，x
- 设x∈Rn
- 用幂法求矩阵的模最大的特征值及其相应的单
- 方程x3-x
- 取步长h=0.2，求解初值问题，用欧拉预
- 有常微分方程的初值问题，试用泰勒展开法，
- 设Ux=d，其中U为三角矩阵。 （a）
- 试用最小二乘法，求解下列超定方程组：
- 设函数f（x）由下表给出：
- 设x*是非线性方程
- 插值型求积公式的求积系数之和（）。
- 用SOR方法解方程组（取ω＝
- 写出求方程4x=cos（x）+1在区间[
- 给定规格化的浮点数系F://β=2，n=