试题详情
- 简答题 已知方程组Ax=b，其中
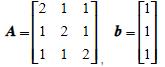（1）列出Jacobi迭代法和Gauss-Seidel迭代法的分量形式； （2）讨论上述两种迭代法的收敛性。
-
（1）Jacobi迭代法：
关注下方微信公众号，在线模考后查看
热门试题
- 分别用二阶显式亚当姆斯方法和二阶隐式亚当
- 已知f（-1）=2，f（1）=3，f（2
- 对于n+1个节点的插值求积公式至少具有（
- （）的3位有效数字是0.236×10
- 设fˊ（-1）=1，fˊ（0）=3，fˊ
- 已知线性方程组 （1）写出雅可比迭代公
- 应用Newton法分别导出求方程
- 为求方程x3-x<
- x=（3，0，-4，12）T<
- 设初值问题 （1）写出用Euler方法
- 证明等式试依据nsin（π/n）（
- 用改进的平方根法解方程组
- 插值型求积公式的求积系数之和=（）。其中
- 设 （1）试求f（x）在上的三次Herm
- 设A与B为n阶矩阵，A为非奇异，考虑解方
- 设xi（i=0，1
- 设x0，x
- 插值型求积公式的求积系数之和（）。
- 若yn=2
- 已知求解线性方程组Ax=b的分量迭代格式