试题详情
- 简答题 用改进的平方根法解方程组
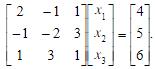
- x=(10/9,7/9,23/9)T。
关注下方微信公众号,在线模考后查看

热门试题
- 下述矩阵能否分解为LU(其中L为单位下三
- 用牛顿法求方程xex
- 在牛顿-柯特斯求积公式:中,当系数是负值
- 设li(x)是以x
- 试写出求方程1/x-c=0(其中c为已知
- 设f(x)可微,求方程x=f(x)的根的
- 已知下列函数表: (1)写出相应的三次
- 已知方程组Ax=b,其中, (1)试讨
- 可以生成上述序列。试考察计算Pn的算法的
- 用改进的尤拉方法解初值问题 取步长h=
- 由下列数表进行Newton插值,所确定的
- 导出如下3个求积公式,并给出截断误差的表
- 已知y=f(x)的数据如下: 求二次插
- 插值型求积公式的求积系数之和()。
- 求f(x)=x4在
- 设为Rn×n上任意
- 证明n阶均差有下列性质:若F(x)=cf
- 在[-1,1]上利用幂级数项数求f(x)
- 矩阵第一行乘以一数,成为 证明当时,c
- 用Romberg方法求,要求误差不超过。