试题详情
- 简答题 设
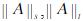为Rn×n上任意两种矩阵算子范数，证明存在常数c1，c2>0，使对一切A∈Rn×n满足 
-
由向量范数的相容性可知存在常数a1，a2>0，使得
，于是令c1=a1/a2>0，c2=a2/a1>0，则对任意A∈Rn×n，均有不等式
关注下方微信公众号，在线模考后查看
热门试题
- 已知f（1）=1.0，f（2）=1.2，
- 求解一阶常微分方程初值问题y&prim
- 研究求的牛顿公式 证明对一切k=1.2
- 证明解y’=f（x，y）的公
- 可以生成上述序列。试考察计算Pn的算法的
- 根据下列f（x）=tanx的数值表：
- 试确定常数A，B，C和α，使
- 求方程x2-x-1
- 若用复化梯形公式计算，要求误差不超过10
- 为求方程x3-x<
- 设f（x）=x4+
- 导出如下3个求积公式，并给出截断误差的表
- 试确定常数A，B，C和a，使得数值积分公
- 用最小二乘法求一个形如y=a+bx
- 设，试说明A为可约矩阵。
- 在[-1，1]上利用插值极小化求f（x）
- 用改进的尤拉方法解 取步长h=0.1计
- 设A为n阶非奇异矩阵且有分解式A=LU，
- 设x=（3，-1，5，8）T<
- 中待定参数Ai的值