试题详情
- 简答题设f(x)=x4+3x3-1,在[0,1]上求三次最佳逼近多项式。
-
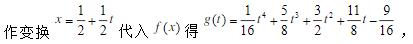
则g(t)在[-1,1]上的三次最佳逼近多项式为
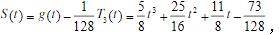
作逆变换t=2x-1代入S(t),则f(x)在[0,1]上的三次最佳逼近多项式为
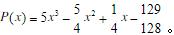
关注下方微信公众号,在线模考后查看

热门试题
- 试用最小二乘法,求解下列超定方程组:
- 设xi(i=0,1
- 计算的Newton迭代格式为()
- 设为Rn×n上任意
- 设假定g是准确的,而对t的测量有±0.1
- 已知函数值f(0)=6,f(1)=10,
- 用二次拉格朗日插值多项式的值。插值节点和
- 分别用二阶显式亚当姆斯方法和二阶隐式亚当
- 试确定常数A,B,C和α,使
- 正方形的边长大约为100cm,应怎样测量
- 已知方程组AX=B,其中 (1)列出J
- 牛顿插值多项式的余项是()
- 将矩阵A分解为单位下三角矩阵L和上三角矩
- 绘图题:画出SOR迭代法的框图。
- 证明矩阵 对于是正定的,而雅可比迭代只
- 用秦九韶法求P(5)。
- 证明:(a)如果A是对称正定阵,则A
- 用雅可比、高斯-塞德尔迭代法,求解方程组
- 给定插值点(xi,
- 设方程组 (a)求解此方程组的雅可比迭