试题详情
- 简答题 设方程组
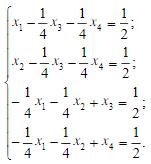（a）求解此方程组的雅可比迭代法的迭代矩阵B0的谱半径； （b）求解此方程组的高斯－塞德尔迭代法的迭代矩阵的谱半径； （c）考察解此方程组的雅可比迭代法及高斯－塞德尔迭代法的收敛性。
-
（a）Jacobi迭代矩阵的谱半径
；
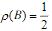（b）Gauss-Seidel迭代矩阵的谱半径ρ（B）=0.25；
（c）两种方法的谱半径均小于1，所以两种方法均收敛。
事实上，对于方程组Ax=b，矩阵A为严格对角占优则Jacobi和Gauss-Seidel迭代法均收敛。 关注下方微信公众号，在线模考后查看
热门试题
- 计算方法实际计算时，对数据只能取有限位表
- 对于给定的线性方程组 （1）讨论雅可比迭
- 用Gauss-Seidel迭代法求解线性
- 取h=0.2，用四阶经典的龙格－库塔方法
- 若用复化辛浦生公式计算积分问至少应将区间
- 简述二分法的优缺点。
- 已知，求Householder阵H使Hx
- Jacobi迭代法解方程组Ax=b的必要
- 证明矩阵 对于是正定的，而雅可比迭代只
- 研究求的牛顿公式 证明对一切k=1.2
- 有常微分方程的初值问题，试用泰勒展开法，
- 给定插值点（xi，
- 已知x=φ（x）在区间[a，b]
- 设detA≠0，用a，b表示解方程
- f（1）=-1，f（2）=2，f（3）=
- 试证{T*
- 已知数据表 （1）构造关于点集和权的正
- 设∥A∥P,∥A∥
- 如果，证明用梯形公式计算积分所得到的结果
- 设方程组 （a）求解此方程组的雅可比迭