试题详情
- 简答题设∥A∥P,∥A∥q为Rn*n上任意两种矩阵（算子）范数，证明存在常数c1,c2>0使得
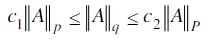对一切A∈Rn*n均成立。
关注下方微信公众号，在线模考后查看
热门试题
- 设Ax=b，其中A为非奇异阵。 （a）
- 序列{yn}满足递
- 用列主元素消元法求解方程组 。
- 用列主元三角分解法求解方程组。其中
- 观测物体的直线运动，得出以下数据，求运动
- 设x=020013753为真值xr=0.
- 设x*的相对误差为
- 用列主元消去法解线性方程组
- 高斯--塞尔德迭代法解线性方程组的迭代格
- 什么是矩阵的条件数？如何判断A是病态的或
- 构造代数精度最高的如下形式的求积公式，并
- 已知函数的一组数据： 求分段线性插值函
- 解方程组Ax=b的简单迭代格式x
- 设矩阵分解为A=LU，则U=（）
- 设f（x）可微，求方程x=f（x）的牛顿
- 设A为n阶矩阵，如果称A为对角优势阵。证
- 已知函数值f（0）=6，f（1）=10，
- 应用Newton法于方程x3<
- 已知一组试验数据如下： 求它的拟合曲线
- 已知求解线性方程组Ax=b的分量迭代格式