试题详情
- 简答题 设A为n阶矩阵，如果
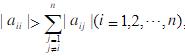称A为对角优势阵。证明：若A是对角优势阵，经过高斯消去法一步后，A具有形式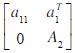 
-
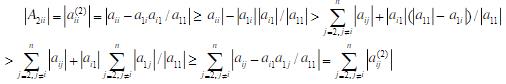
则A2是对角优势阵，故高斯消去法与部分选主元高斯消去法对于对称的对角优势阵每一步均选取同样的主元，得出的是同样的结果。 关注下方微信公众号，在线模考后查看
热门试题
- 给定函数f（x），设对一切x，f&pri
- 求f（x）=sinx在[0，π/2]上的
- 用直接三角分解（Doolittle）法解
- 面Matlab程序所求解的数学问题是（）
- 已知f（1）=1.0，f（2）=1.2，
- 若用二分法求方程f（x）=0区间[1，2
- 计算，取≈1.4，利用下列等
- 以下各表示的近似数，问具有几位有效数字？
- 欲使线性插值具有4位有效数字。在区间[0
- 设是[0，1]区间上带权的最高次幂项系数
- 实数a≠0，考察矩阵，试就方程组A
- 设f（x）=（x3
- 根据下面给出的函数的数据表，分别用复合梯
- 在[a，b]上求插值多项式H3
- 设，试说明A为可约矩阵。
- 利用积分计算ln4时，若采用复化梯形公式
- 设，在−1≤x≤
- 高斯--塞尔德迭代法解线性方程组的迭代格
- 用Romberg方法求，要求误差不超过。
- 给定规格化的浮点数系F://β=2，n=