试题详情
- 简答题 给定函数f（x），设对一切x，f′（x）存在，而且
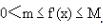，证明对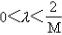
的任意常数λ，迭代法xk+1=xk-λf（xk）均收敛于方程f（x）=0的根。
-
如下：
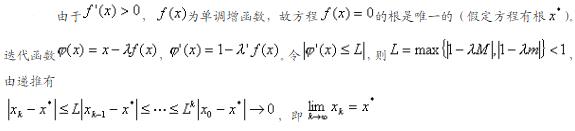
关注下方微信公众号，在线模考后查看
热门试题
- 用追赶法求解三对角方程组
- 求f（x）=x4在
- 解常微分方程初值问题的梯形格式是（）阶方
- 设一阶差商f（x1
- 证明解y’=f（x，y）的公
- 用欧拉方法求在点x=0.5，1.0，1.
- 用二分法求解方程f（x）=x3
- 用带位移的QR方法计算 全部特征值。
- 用三点公式和五点公式分别求在x=1.0，
- 用3点Gauss-Legendre公式求
- 试用“追赶法”解
- 试确定常数A，B，C和a，使得数值积分公
- 用1+近似表示所产生的误差是（）误差。
- 用复化梯形公式求积分，问要将积分区间[a
- 牛顿插值多项式的余项是（）
- 现给出一张记录{xk
- 设f（x）=（x3-a）2<
- 设M3=Span{
- 给定迭代过程，x（k+1）
- 已知f（1）=1.0，f（2）=1.2，