试题详情
- 简答题 应用Newton法于方程x3-a=0，求立方根
的迭代公式，并讨论其收敛性。
-
方程x3-a=0的根x*=
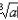，用Newton迭代法
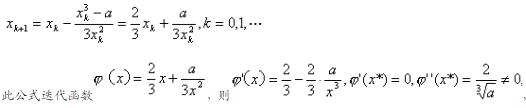
故迭代法2价收敛。 关注下方微信公众号，在线模考后查看
热门试题
- 设A=（aij）&
- 若f（x）=a0+
- 已知sinx区间[0.4，0.8]的函数
- 等距二点求导公式f′（x1）≈（）
- 求矩阵 与特征值4对应的特征向量。
- 梯形公式具有1次代数精度，Simpson
- 求参数a，b，使得计算初值问题的二步数值
- 令Tn（x）=T<
- 求a，b使为最小。
- 方阵T分块形式为 其中Tii
- 用Romberg方法求，要求误差不超过。
- 用插值法求满足以下条件的不超过三次的插值
- 改变函数的形式，使计算结果较精确（）。
- 设A为不可约弱对角优势阵且0<ω≤1，求
- 设x1=1.216
- 求证的充要条件是对任何向量x，都有
- 用LU分解法求解线性方程组
- 用劈因子法解方程x3
- 用1+近似表示所产生的误差是（）误差。
- 设f（1）=1，f（2）=2，f（3）=