试题详情
- 简答题 若f(x)=a0+a1x+...+an-1xn-1+anxn有n个不同实根x1,x2,...,xn,证明:
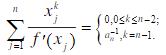
-
由于x1,x2,...,xn是f(x)的n个互异的零点,所以

关注下方微信公众号,在线模考后查看

热门试题
- 若x=e≈2.71828=x*
- 设∥A∥P,∥A∥
- x*为精确值x的
- 试推导矩阵A的Crout分解A=LU的计
- 高斯--塞尔德迭代法解线性方程组的迭代格
- 设x=020013753为真值xr=0.
- 求解一阶常微分方程初值问题y&prim
- 计算球体积要使相对误差限为1%,问度量半
- 设f(x)=(x3-a)2<
- 设f(x)∈C[a,b],把[a,b]分
- (a)设A是对称阵且a11
- 设方程组 证明解此方程的Jacobi迭
- 数值积分公式是否为插值型求积公式,为什么
- 可以生成上述序列。试问计算的上述公式是稳
- 若f(x)=a0+
- 设计一个计算的牛顿迭代法,且不用除法(其
- 设x∈Rn
- 编出改进FFT算法的程序框图。
- 利用Gauss变换阵,求矩阵的LU分解。
- 用高斯-塞德尔方法解方程组取,迭代三次(