试题详情
- 简答题 利用Gauss变换阵，求矩阵
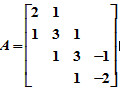的LU分解。
-
关注下方微信公众号，在线模考后查看
热门试题
- 对f（x）=sinx在[0，π/2]上求
- 导出具有下列形式的三阶方法：
- 给定求积公式试确定a，b，c使它的代数精
- 试用复化梯开公式计算曲线f（x）=tan
- 取h=0.25，用差分方法解边值问题。
- 如果f（x）是m次多项式，记，证明f（x
- 近似值x*=0.2
- 对于n+1个节点的插值求积公式至少具有（
- L为阶的上三角阵，试计算用回代算法解上三
- 用改进的欧拉公式，求以下微分方程 的数
- 用追赶法求解三对角方程组
- 设初值问题 a）写出由Euler方法、取
- 试用消元法解方程组假定只用三位数计算，问
- 已知数e=2.718281828...，
- 用改进的Euler法解初值问题取步长h=
- 给定规格化的浮点数系F://β=2，n=
- 用n=8的复化梯形公式（或复化&ensp
- 设li（x）是以x
- 确定求积公式的待定参数，使其代数精度尽量
- 写出求解方程组的Gauss-Seidel