试题详情
- 简答题 取h=0.25,用差分方法解边值问题。
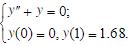
-
用差商逼近导数的方法把原边值问题转化为等价差分法方程组可得,
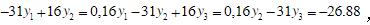
解此方程组可得
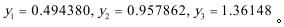
关注下方微信公众号,在线模考后查看

热门试题
- 用简单迭代法求方程f(x)=0的实根,把
- 证明两点三次埃尔米特插值余项是 并由此求
- 面Matlab程序所求解的数学问题是()
- 用列主元消去法求解方程组 并求出系数矩
- 设初值问题 a)写出由Euler方法、取
- 用最小二乘原理求一个形如y=a+bx
- 用Gauss-Seidel迭代法求解线性
- 求f(x)=x4在
- 求f(x)=sinx在[0,π/2]上的
- 设f(x)=(x3
- 证明解y’=f(x,y)的公
- 证明:若为严格对角占优矩阵,则A非奇异。
- 已知方程组Ax=b,其中, (1)试讨
- 对一元2次方程具有5位有效数字,求其具有
- 已知,求Householder阵H使Hx
- 用列主元三角分解法求解方程组。其中
- 用雅可比、高斯-塞德尔迭代法,求解方程组
- 数值积分公式是否为插值型求积公式,为什么
- 设x=(3,-1,5,8)T<
- 取h=0.25,用差分方法解边值问题。