试题详情
- 简答题 用Gauss-Seidel迭代法求解线性方程组
取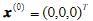
，列表计算三次，保留三位小数。
-
Gauss-Seidel迭代格式为：
关注下方微信公众号，在线模考后查看
热门试题
- 观测物体的直线运动，得出以下数据，求运动
- 设A∈Rn×n，求
- 给定函数f（x），设对一切x，f′（x）
- 用高斯-塞德尔方法解方程组取，迭代四次（
- 设已知一组实验数据
- 用幂法计算下列矩阵的主特征值及对应的特征
- 求A、B使求积公式的代数精度尽量高，并求
- 观测物体的直线运动，得出以下数据：
- 梯形公式具有1次代数精度，Simpson
- x*为精确值x的
- -324.7500是舍入得到的近似值，它
- 通过点（x0，y<
- 近似值x*=0.2
- 方程组Ax=b，其中，A是对称的且非奇异
- 利用区间变换推出区间为[a，b]的伯恩斯
- 用梯形方法解初值问题 证明其近似解为
- 导出如下3个求积公式，并给出截断误差的表
- 解常微分方程初值问题的梯形格式是（）阶方
- 用Newton法求下列方程的根，计算准
- π=3.14159...具有4位有效数字