试题详情
- 单项选择题通过点(x0,y0)的拉格朗日插值基函数l0(x),l1(x)满足()
A、
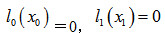
B、

C、

D、

- D
关注下方微信公众号,在线模考后查看

热门试题
- 用下列方法求f(x)=x3<
- 设 证明:即使级数I+A+A
- 什么是Lagrange插值基函数?它们有
- 推导下列三种矩形求积公式:
- 确定求积公式中的待定参数,使其代数精确度
- 确定求积公式中的待定参数,使其代数精确度
- 利用反幂法求矩阵的最接近于6的特征值及对
- 试写出求方程1/x-c=0(其中c为已知
- 求矛盾方程组:的最小二乘解。
- 已知高斯求积公式将区间[0,1]二等分,
- 计算,取≈1.4,利用下列等
- 证明对于任意选择的A,序列收敛于零
- 证明梯形公式和辛普森公式当n→
- 求证的充要条件是对任何向量x,都有
- 试确定常数A,B,C和a,使得数值积分公
- 试讨论用Jacobi迭代法和Gauss-
- 取5个等距节点 ,分别用复化梯
- 在-4≤x≤4上给出f(x)=e
- 设A∈Rn×n为对
- 设x1=1.216