试题详情
- 简答题 证明梯形公式和辛普森公式当n→∞时收敛到积分
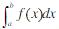 。
。
-
梯形公式和辛甫森公式的余项分别为

关注下方微信公众号,在线模考后查看

热门试题
- 设A为n阶矩阵,如果称A为对角优势阵。证
- Hermite插值与Lagrange插值
- 取步长h=0.2,求解初值问题,用欧拉预
- 用Gauss-Seidel迭代法求解线性
- 构造代数精度最高的如下形式的求积公式,并
- 改变函数的形式,使计算结果较精确()。
- 证明:若为严格对角占优矩阵,则A非奇异。
- 若线性代数方程组AX=b的系数矩阵A为严
- 已知下列函数表: (1)写出相应的三次
- 证明:梯形公式 无条件稳定。
- 如何选取r,使p(x)=x2<
- 根据下列f(x)=tanx的数值表:
- 将下列方程化为一阶方程组:
- 设f(x)=1/(1+x2
- 分析下列方程各存在几个根,并找出每个根的
- 推导下列三种矩形求积公式:
- 取h=0.2用差分方法解边值问题
- 令║·║是Rn<
- 用插值极小化方法求在[1,2]上的二次插
- 设空间φ1=spa