试题详情
- 简答题 将下列方程化为一阶方程组:
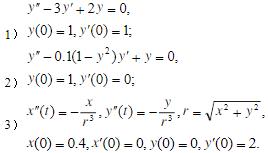
-
如下:
关注下方微信公众号,在线模考后查看

热门试题
- 试用消元法解方程组假定只用三位数计算,问
- 已知,求Householder阵H使Hx
- 推导下列三种矩形求积公式:
- 设方程组 迭代公式为
- 用龙贝格方法计算积分,要求误差不超过10
- 改变函数的形式,使计算结果较精确()。
- 求矩阵 与特征值4对应的特征向量。
- ,则A的谱半径ρ(A)=(),A
- 取步长h=0.1,求解初值问题用改进的欧
- 构造求解方程ex+
- 为求x3-5x-3
- 证明
- 设计算A的行范数,列范数,2-范数及F-
- 用SOR方法解方程组(分别取松弛因子&o
- 等距二点求导公式f′(x1)≈()
- 写出立方根的牛顿迭代公式()。
- 设f(x)=C2[
- 有常微分方程的初值问题,试用泰勒展开法,
- 设假定g是准确的,而对t的测量有±0.1
- 应用牛顿法于方程f(x)=xn