试题详情
- 简答题 用龙贝格方法计算积分
，要求误差不超过10-5。
-
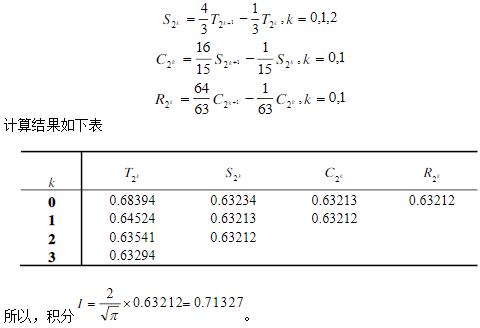
首先算出T1，T2，T4，T8，然后逐次应用3个加速公式
关注下方微信公众号，在线模考后查看
热门试题
- 什么是求积公式的代数精确度？如何利用代数
- 若用复化辛浦生公式计算积分问至少应将区间
- 已知方程组Ax=b，其中 （1）列出J
- 用牛顿法求的近似值，取x0
- 则=（），=（），=（），=（）。
- 求矩阵 与特征值4对应的特征向量。
- 设假定g是准确的，而对t的测量有±0.1
- 设初值问题y′=x
- 已知，则A的谱半径ρ（A）=（）
- 用高斯消去法解方程组
- 利用尤拉方法计算积分 在点x=0.5，1
- 对于初值问题，证明当h<0.2时，欧拉公
- 设xi（i=0，1
- 若x1≈0.937具有3位有
- 设x*的相对误差为
- 求矛盾方程组：的最小二乘解。
- 用二分法和牛顿法求x-tgx=0的最小正
- 设f（x）可微，求方程x=f（x）的根的
- 数值求积公式的代数精度为（）
- 用牛顿法求方程xex