试题详情
- 简答题 用高斯消去法解方程组
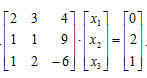
-

关注下方微信公众号,在线模考后查看

热门试题
- 求解方程组的高斯—塞德尔迭代
- 写出求解下列方程组的Jacobi迭代格式
- 卫星轨道是一个椭圆,椭圆周长的计算公式是
- 梯形公式具有1次代数精度,Simpson
- 已知一组试验数据如下: 求它的拟合曲线
- 应用牛顿法于方程x2
- 设方程组 证明解此方程的Jacobi迭
- 利用公式求下列各近似值的误差限: 其中
- 解初值问题的改进欧拉法是()阶方法。
- 已知x=[0,-1,2]T
- 试确定常数A,B,C和α,使
- 设求方程f(x)=0的根的牛顿法收敛,则
- 实数a≠0,考察矩阵,试就方程组A
- 用复化梯形公式求积分,问要将积分区间[a
- 证明
- 用列主元消元法解线性方程组作第一次消元后
- 若x1≈0.937具有3位有
- 求满足下列条件的埃尔米特插值多项式:
- 直接验证柯特斯公式具有5次代数精度。
- 设f(x)=C2[