试题详情
- 简答题什么是求积公式的代数精确度？如何利用代数精确度的概念去确定求积公式中的待定参数？
-
一个求积公式
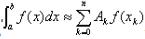如果当f（x）为任意m次多项式时，求积公式精确成立，而当f（x）为次数大于m次多项式时，它不精确成立，则称此求积公式具有m次代数精确度。根据定义只要令f（x）=xi（i=0，1，...，m）代入求积公式两端，公式成立，得含待定参数的m+1个方程的方程组，这里m+1为待定参数个数，解此方程组则为所求。
关注下方微信公众号，在线模考后查看
热门试题
- 用最小二乘原理求一个形如y=a+bx
- 写出求解下列方程组的Jacobi迭代格式
- 设初值问题 （1）写出用Euler方法
- 根据下面给出的函数的数据表，分别用复合梯
- 求方程x3-x
- 导出如下3个求积公式，并给出截断误差的表
- 已知函数值f（0）=6，f（1）=10，
- 对矩阵，求||A||&infi
- 说明方程在区间[1，2]内有惟一根x
- 试确定常数A，B，C和a，使得数值积分公
- 如下函数值表 建立不超过三次的牛顿插值
- 试划出部分选主元素三角分解法框图，并且用
- 如何选取r，使p（x）=x2<
- 已知y=f（x）的数据如下： 求二次插
- 用Gauss消去法求解下列方程组。
- 有常微分方程的初值问题，试用泰勒展开法，
- 确定求积公式中的待定参数，使其代数精确度
- 设 计算A的条件数。cound（A）<
- 用改进的尤拉方法解 取步长h=0.1计
- 设函数f（x）由下表给出：