试题详情
- 简答题 用高斯-塞德尔方法解方程组
取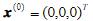
，迭代四次（要求按五位有效数字计算）。
-
迭代格式
关注下方微信公众号，在线模考后查看
热门试题
- 用二分法求方程x3
- 已知方程x3-x<
- 已知，用抛物线插值计算的值并估计截断误差
- 证明：梯形公式 无条件稳定。
- 试用初等反射阵A分解为QR，其中Q为正交
- 确定求积公式中的待定参数，使其代数精确度
- 如果用二分法求方程x3
- 已知方程组AX=f，其中 （1）列出J
- 设xj为互异节点（
- 求证的充要条件是对任何向量x，都有
- 用高斯-塞德尔方法解方程组取，迭代三次(
- 求f（x）=sinx在[0，π/2]上的
- 分别用2.718281，2.718282
- 以100，121，144为插值节点，用插
- 将矩阵A分解为单位下三角矩阵L和上三角矩
- 利用尤拉公式求解初值问题，其中步长h=0
- 设求方程f（x）=0的根的牛顿法收敛，则
- 用幂法求矩阵的模最大的特征值及其相应的单
- 利用矩阵的LU分解法解方程组
- 给定函数f（x），设对一切x，f′（x）