试题详情
- 简答题 利用矩阵的LU分解法解方程组
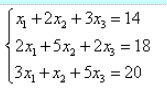
-
关注下方微信公众号,在线模考后查看

热门试题
- 实数a≠0,考察矩阵,试就方程组A
- 写出求解下列方程组的Jacobi迭代格式
- 设A∈Rn×n为对
- 用插值法求满足以下条件的不超过三次的插值
- n次插值型求积公式至少具有()次代数精度
- 设(1)方程f(x)=0有根x*: (2
- 若f(x)∈C2
- ()的3位有效数字是0.236×10
- 试用列主元Gauss消去法解下列方程组:
- 用四阶龙格-库塔法求解初值问题,取h=0
- 求证的充要条件是对任何向量x,都有
- 如果方阵A有aij
- 证明定积分近似计算的抛物线公式: 具有
- 方阵T分块形式为 其中Tii
- 已知常微分方程的初值问题: 用改进的Eu
- 3.141580是π的有()位有效数字的
- 求解方程组的高斯—塞德尔迭代
- 设矩阵分解为A=LU,则U=()
- ,则=(),A的谱半径ρ(A)=
- 取h=0.2用差分方法解边值问题