试题详情
- 简答题 方阵T分块形式为
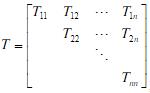其中Tii（i=1，2，...，n）为方阵，T称为块上三角阵，如果对角块的阶数至多不超过2，则称T为准三角形形式，用σ（T）记矩阵T的特征值集合，证明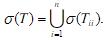 
-
关注下方微信公众号，在线模考后查看
热门试题
- 求解方程组的高斯—塞德尔迭代
- 设方程组 迭代公式为
- 以100，121，144为插值节点，用插
- 设x=（1，9，-5，2）T<
- f（x）是[-a，a]上的连续奇（偶）函
- 设f（x）可微，求方程x=f（x）的牛顿
- 分别用梯形公式和辛普森公式计算下列积分：
- 试用复化梯开公式计算曲线f（x）=tan
- 试推导矩阵A的Crout分解A=LU的计
- l0（x），l
- 已知，则A的谱半径ρ（A）=（）
- 比较求ex+10x
- 证明解线性方程组Ax=b的雅可比迭代收敛
- 根据下列f（x）=tanx的数值表：
- 以下各数均为有效数字： （1）0.106
- 设x的相对误差为a%，求y=x
- L为阶的上三角阵，试计算用回代算法解上三
- 设方程组 证明解此方程的Jacobi迭
- ，则A的谱半径ρ（A）=（），A
- 写出求解下列方程组的Jacobi迭代格式