试题详情
- 简答题 分别用梯形公式和辛普森公式计算下列积分:
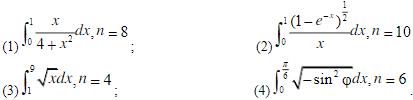
-
如下:

关注下方微信公众号,在线模考后查看

热门试题
- 证明解线性方程组Ax=b的雅可比迭代收敛
- 用辛普森公式求积分并计算误差
- 设x=(x1,x2,L,xn)
- 应用牛顿法于方程,导出求的迭代公式,并用
- 写出求解方程组的Gauss-Seidel
- 对于给定的线性方程组 (1)讨论雅可比迭
- 已知求解常微分方程初值问题的数值格式为
- 已知近似值xA=2
- 已知x=φ(x)在区间[a,b]
- 将下列方程化为一阶方程组:
- 若则矩阵A的谱半径ρ(A)=()
- 设Ax=b,其中A为非奇异阵。 (a)
- 取步长h=0.1,求解初值问题用改进的欧
- 若线性代数方程组AX=b的系数矩阵A为严
- 设xj为互异节点(
- 用直接三角分解(Doolittle)法解
- 设A为非奇异矩阵,求证
- 如下函数值表 建立不超过三次的牛顿插值
- 为求方程x3―x<
- 令Tn(x)=T<