试题详情
- 简答题 应用牛顿法于方程
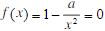，导出求
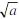的迭代公式，并用此公式求
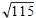的值。
-
取a=115，x0=10，迭代三次得
关注下方微信公众号，在线模考后查看
热门试题
- 证明：如果A是正交阵，则cound（A）
- 设Ax=b，其中A为非奇异阵。 （a）
- 用复化Simpson公式计算积分的近似值
- 设f（x）=x4+
- 用二分法求方程x2
- 插值型求积公式的求积系数之和（）。
- 试确定常数A，B，C和α，使
- 用n=8的复化梯形公式（或复化&ensp
- 求满足下列条件的埃尔米特插值多项式：
- 求f（x）=x4在
- 证明两点三次埃尔米特插值余项是 并由此求
- 导常微分方程的初值问题的数值解公式：
- 如果方阵A有aij
- 解常微分方程初值问题的梯形格式是（）阶方
- 试确定常数A，B，C和a，使得数值积分公
- 已知a=1.2031，b=0.978是经
- 用高斯-塞德尔方法解方程组取，迭代三次(
- 编出用正交多项式做最小二乘拟合的程序框图
- 证明下列两种龙格－库塔方法是三阶的：
- 设A为n阶矩阵，如果称A为对角优势阵。证