试题详情
- 简答题 用高斯-塞德尔方法解方程组
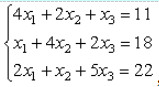取
，迭代三次(要求按五位有效数字计算).。
-
关注下方微信公众号，在线模考后查看
热门试题
- 编出改进FFT算法的程序框图。
- 设有函数值表：
- 如果方阵A有aij
- 设方程组 （a）求解此方程组的雅可比迭
- 就初值问题y′=ax+b，y
- 在[-1，1]上利用插值极小化求f（x）
- 已知函数的一组数据： 求分段线性插值函
- 已知f（-1）=2，f（1）=3，f（2
- 设x∈Rn
- 写出求方程4x=cos（x）+1在区间[
- 设x=020013753为真值xr=0.
- 用辛浦生公式计算积分近似值；
- 已知，用抛物线插值计算的值并估计截断误差
- 设Y0=28，按递
- 对初值问题证明用梯形公式所求得的近似值为
- 设li（x）是以x
- 用1+近似表示所产生的误差是（）误差。
- 面Matlab程序所求解的数学问题是（）
- 给出lnx的函数表如下： 试用线性插值
- 已知数值积分公式为： 试确定积分公式中