试题详情
- 简答题在[-1,1]上利用插值极小化求f(x)=tg-1x的三次近似最佳逼近多项式。
-

做插值节点可求得三次近似最佳逼近多项式为
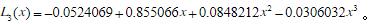
关注下方微信公众号,在线模考后查看

热门试题
- 设f(x)=4x5
- 设方程组 试考察解此方程组的雅可比迭代
- Hermite插值与Lagrange插值
- 在[-1,1]上利用幂级数项数求f(x)
- L为阶的上三角阵,试计算用回代算法解上三
- 已知近似值xA=2
- 设f(x)=x4+
- 设f(x)=sinπx.,求f(x)于[
- 设A为非奇异矩阵,且,求证(A+&del
- 用列主元三角分解法求解方程组。其中
- 试建立一种收敛的Seidel迭代公式,说
- 设 已知方程组Ax=b的精确解为 (1)
- 设fˊ(-1)=1,fˊ(0)=3,fˊ
- 利用尤拉方法计算积分 在点x=0.5,1
- 近似值x*=0.2
- 已知线性方程组 (1)写出雅可比迭代公
- 设一阶差商f(x1
- 用直接三角分解(Doolittle)法解
- 设计算A的行范数,列范数,2-范数及F-
- 设detA≠0,用a,b表示解方程