试题详情
- 简答题 设A为非奇异矩阵，且
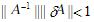，求证（A+δA）-1存在且有估计 
-
关注下方微信公众号，在线模考后查看
热门试题
- 考察下列求积公式具有几次代数精度：
- 对一元2次方程具有5位有效数字，求其具有
- 有常微分方程的初值问题，试用泰勒展开法，
- 已知常微分方程的初值问题： 用改进的Eu
- 确定求积公式中的待定参数，使其代数精确度
- 方程x3-x
- 证明对于任意选择的A，序列收敛于零
- 证明下列两种龙格－库塔方法是三阶的：
- 证明定积分近似计算的抛物线公式： 具有
- 用SOR方法解方程组（分别取松弛因子&o
- 画图说明牛顿迭代公式的几何意义。
- 插值型求积公式的求积系数之和=（）。其中
- 矩阵满足什么条件才能使A的LU分解存在唯
- 取≈1.732计算，下列方法
- 高斯--塞尔德迭代法解线性方程组的迭代格
- 写出求解方程组的Gauss-Seidel
- 用二分法求方程x2
- 用牛顿法求方程xex
- 若则矩阵A的谱半径ρ（A）=（）
- 通过四个互异节点的插值多项式p（x），只