试题详情
- 简答题用二分法求方程x2-x-1=0的正根,使误差小于0.05。
-
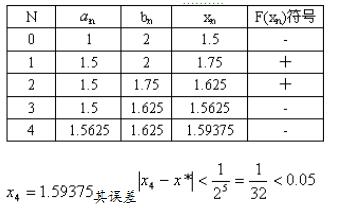
使用二分法先要确定有根区间[a,b]。本题f(x)=x2-x-1=0,因f(1)=-1,f(2)=1,故区间[1,2]为有根区间。另一根在[-1,0]内,故正根在[1,2]内。用二分法计算各次迭代值如表。
关注下方微信公众号,在线模考后查看

热门试题
- 构造代数精度最高的如下形式的求积公式,并
- 数值积分公式是否为插值型求积公式,为什么
- 通过点(x0,y<
- 给定函数f(x),设对一切x,f&pri
- 说明方程在区间[1,2]内有惟一根x
- 数值微分中,已知等距节点的函数值(x<
- 解非线性方程f(x)=0的牛顿迭代法具有
- 写出求方程4x=cos(x)+1在区间[
- 在牛顿-柯特斯求积公式:中,当系数是负值
- 用下列方法计算积分比较结果 (1)龙贝格
- 设f(x)∈C[a,b],把[a,b]分
- 用列主元消元法解线性方程组作第一次消元后
- f(x)=x7+x
- 用二分法求方程的正根,要求误差小于0.0
- 用高斯-塞德尔方法解方程组取,迭代三次(
- 若用复化辛浦生公式计算积分问至少应将区间
- 以下各数均为有效数字: (1)0.106
- 用欧拉方法求在点x=0.5,1.0,1.
- 确定下列公式中的待定参数,使其代数精度尽
- 试讨论用Jacobi迭代法和Gauss-