试题详情
- 简答题 写出求解方程组
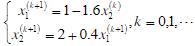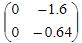的Gauss-Seidel迭代分量形式（），迭代矩阵为（），此迭代法是否收敛（）。
-
；
；收敛
关注下方微信公众号，在线模考后查看
热门试题
- 导出具有下列形式的3阶方法：
- 利用反幂法求矩阵的最接近于6的特征值及对
- 将矩阵A分解为单位下三角矩阵L和上三角矩
- 求矩阵 与特征值4对应的特征向量。
- 对方程组 （1）试建立一种收敛的Sei
- 用带位移的QR方法计算 全部特征值。
- 假设f（x）在[a，b]上连续，求f（x
- 推导下列三种矩形求积公式：
- 用追赶法求解三对角方程组
- 设 已知方程组Ax=b的精确解为 （1）
- 设x*的相对误差为
- 利用区间变换推出区间为[a，b]的伯恩斯
- 已知求解线性方程组Ax=b的分量迭代格式
- 就初值问题y′=ax+b，y
- 试用复化梯开公式计算曲线f（x）=tan
- 已知下列函数表： （1）写出相应的三次
- -324.7500是舍入得到的近似值，它
- 可以生成上述序列。试考察计算Pn的算法的
- 应用牛顿法于方程f（x）=xn
- 求函数y=在区间[0，1]上的二次插值多