试题详情
- 简答题 将矩阵A分解为单位下三角矩阵L和上三角矩阵U，其中
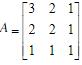，然后求解该方程组
。
-
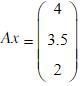如下：
关注下方微信公众号，在线模考后查看
热门试题
- 已知一组试验数据 试用直线拟合这组数据
- 导出如下3个求积公式，并给出截断误差的表
- 利用Gauss变换阵，求矩阵的LU分解。
- 方程组Ax=b，其中，A是对称的且非奇异
- 设f（x）=3x2
- 由高斯消去法说明当Δi
- 设x=（11，0，5，1）T<
- 假设测得一个圆柱体容器的底面半径和高分别
- 确定求积公式中的待定参数，使其代数精确度
- 近似值x*=0.2
- 已知x=[0，-1，2]T
- 用直接三角分解（Doolittle）法解
- 用幂法计算下列矩阵的主特征值及对应的特征
- 给出cos x，0°≦x≦90°的函数表
- 考虑方程组： （a）用高斯消去法解此方
- 设计算A的行范数，列范数，2-范数及F-
- 对初值问题证明用梯形公式所求得的近似值为
- 实数a≠0，考察矩阵，试就方程组A
- 高斯--塞尔德迭代法解线性方程组的迭代格
- ，求f（30）的值.若开平方用六位函数表