试题详情
- 简答题设f(x)可微,求方程x=f(x)的牛顿迭代格式是()。
-
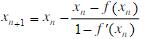
关注下方微信公众号,在线模考后查看

热门试题
- 有常微分方程的初值问题,试用泰勒展开法,
- 设方程组 试考察解此方程组的雅可比迭代
- 已知f(1)=1,f(3)=5,f(5)
- 设 求∥A∥∞<
- 已知f(-1)=2,f(1)=3,f(2
- 由下列数表进行Newton插值,所确定的
- 设f(x)∈C2
- 写出求解方程组的Gauss-Seidel
- 选择a,使积分取得最小值
- n=3,用复合梯形公式求的近似值(取四位
- 设x>0,x的相对误差为δ,求lnx的误
- 对于给定的线性方程组 (1)讨论雅可比迭
- 已知数值积分公式为: 试确定积分公式中
- 利用矩阵的LU分解法解方程组
- 设计一个计算的牛顿迭代法,且不用除法(其
- 求方程x2-56x
- 证明迭代公式是计算的三阶方法。假定初值x
- 设Y0=28,按递
- 将f(x)=sin(x/2)在[-1,1
- 试划出部分选主元素三角分解法框图,并且用