试题详情
- 简答题 设计一个计算
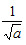的牛顿迭代法，且不用除法（其中a>0）。
-
关注下方微信公众号，在线模考后查看
热门试题
- 利用矩阵的LU分解法解方程组
- 设A为非奇异矩阵，求证
- ，则=（），A的谱半径ρ（A）=
- 用n=8的复化梯形公式（或复化&ensp
- 试讨论用Jacobi迭代法和Gauss-
- 方阵T分块形式为 其中Tii
- 设A为不可约弱对角优势阵且0<ω≤1，求
- 给定插值点（xi，
- 计算方法实际计算时，对数据只能取有限位表
- 将下列方程化为一阶方程组：
- 用列主元消去法解线性方程组，第1次消元，
- 写出求解下列方程组的Jacobi迭代格式
- 画图说明牛顿迭代公式的几何意义。
- 求矩阵 与特征值4对应的特征向量。
- 确定求积公式中的待定参数，使其代数精确度
- 确定下列求积公式中的待定参数，使其代数精
- 证明对于任意选择的A，序列收敛于零
- 构造代数精度最高的如下形式的求积公式，并
- 用复化Simpson公式计算积分的近似值
- 用改进的欧拉公式，求以下微分方程 的数