试题详情
- 简答题 已知方程组AX=f，其中
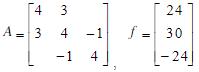（1）列出Jacobi迭代法和Gauss-Seidel迭代法的分量形式。 （2）求出Jacobi迭代矩阵的谱半径。
-
如下：
关注下方微信公众号，在线模考后查看
热门试题
- 求证：当m≤f（x）≤M时，当m≤B
- 若x=e≈2.71828=x*
- 已知高斯求积公式将区间[0，1]二等分，
- 通过点（x0，y<
- 求证： （a）║x║&infi
- 利用Gauss变换阵，求矩阵的LU分解。
- 求f（x）=sinx在[0，π/2]上的
- 设A是对称正定矩阵，经过高斯消去法一步后
- 用列主元消元法解线性方程组作第一次消元后
- 若f（x）=3x4
- 设方程组 （a）求解此方程组的雅可比迭
- 试分别求出用Jacobi迭代法和Gaus
- 假设f（x）在[a，b]上连续，求f（x
- 已知三角形面积，其中c为弧度，，且测量a
- 用二分法求方程f（x）=x3<
- 分别描述R2中（画
- 用二分法求方程x2
- 用辛浦生公式计算积分近似值；
- 设矩阵分解为A=LU，则U=（）
- 方程组Ax=b，其中，A是对称的且非奇异