试题详情
- 简答题试分别求出用Jacobi迭代法和Gauss-Seidel迭代法解方程组
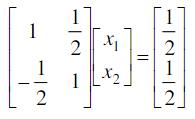的第k次迭代误差的一般表达式。方程组的精确解为x*=[1,1]T。
关注下方微信公众号，在线模考后查看
热门试题
- 证明对任意参数t，下列龙格－库塔公式是二
- 用列主元消去法求解方程组 并求出系数矩
- 证明：若为严格对角占优矩阵，则A非奇异。
- f（x）是[-a，a]上的连续奇（偶）函
- 高斯--塞尔德迭代法解线性方程组的迭代格
- L为阶的上三角阵，试计算用回代算法解上三
- 为求方程x3-x<
- 牛顿插值多项式的余项是（）
- 观测物体的直线运动，得出以下数据，求运动
- 设A=（aij）&
- 方程求根的Newton法是如何推出的？它
- 设f（x）=x7+
- 设初值问题y′=x
- 如有下列表函数： 则一次差商f[0.2
- 为求x3-5x-3
- 设矩阵的A=LU，则U=（）。
- 利用区间变换推出区间为[a，b]的伯恩斯
- 给定迭代过程，x（k+1）
- 对方程组 （1）试建立一种收敛的Sei
- 如有下列表函数： 试计算此列表函数的差