试题详情
- 简答题 分别描述R2中(画图)
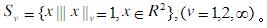
-
关注下方微信公众号,在线模考后查看

热门试题
- 证明对称矩阵 用雅可比迭代法求解方程组A
- 证明等式试依据nsin(π/n)(
- 已知: 分别用拉格朗日插值法和牛顿插值
- 证明
- 方程组Ax=b,其中,A是对称的且非奇异
- 设x0,x
- ()的3位有效数字是0.236×10
- 已知高斯求积公式将区间[0,1]二等分,
- 分别用梯形公式和辛普森公式计算下列积分:
- 有一圆柱,高为25.00cm,半径为20
- 设x*是非线性方程
- 利用积分计算ln4时,若采用复化梯形公式
- 若f(x)∈C2
- 通过四个互异节点的插值多项式p(x),只
- 若x=e≈2.71828=x*
- 用插值法求满足以下条件的不超过三次的插值
- 已知函数值f(0)=6,f(1)=10,
- 考察下列求积公式具有几次代数精度:
- 用Gauss-Seidel迭代法解方程组
- 设An-1是由豪