试题详情
- 简答题 试用初等反射阵A分解为QR,其中Q为正交阵,R为上三角阵,

-
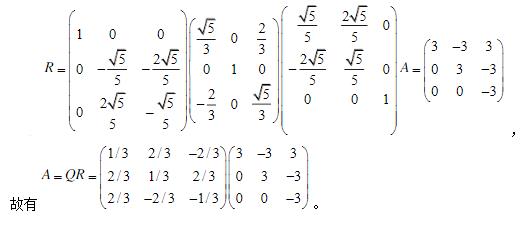
关注下方微信公众号,在线模考后查看

热门试题
- 计算球体积要使相对误差为1%,问度量半径
- 利用尤拉公式求解初值问题,其中步长h=0
- 给出矩阵(a为实数),试分别求出a的取值
- 数值微分中,已知等距节点的函数值(x<
- 试用列主元Gauss消去法解下列方程组:
- 迭代法的收敛条件是(1)(),(2)()
- 设A与B为n阶矩阵,A为非奇异,考虑解方
- 利用矩阵的LU分解法解方程组
- 序列{yn}满足递
- 已知方程组Ax=b,其中, (1)试讨
- 设f(x)=1/(1+x2
- 说明方程在区间[1,2]内有惟一根x
- 设A为不可约弱对角优势阵且0<ω≤1,求
- 导出具有下列形式的3阶方法:
- 计算球的体积,为了使体积的相对误差限为1
- 对于f(x)=0的牛顿公式, 证明收敛到
- 用Gauss消去法求解下列方程组。
- π=3.14159...具有4位有效数字
- 证明定积分近似计算的抛物线公式: 具有
- 有常微分方程的初值问题,试用泰勒展开法,