试题详情
- 简答题 设初值问题
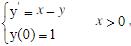 a)写出由Euler方法、取步长h=0.1解上述初值问题数值解的公式; b)写出由改进Euler方法、取步长h=0.1解上述初值问题数值解的公式。
a)写出由Euler方法、取步长h=0.1解上述初值问题数值解的公式; b)写出由改进Euler方法、取步长h=0.1解上述初值问题数值解的公式。
-
如下:

关注下方微信公众号,在线模考后查看

热门试题
- 用二分法求方程的正根,要求误差小于0.0
- 用二分法求方程x2
- 用下列方法计算积分比较结果 (1)龙贝格
- 证明梯形公式和辛普森公式当n→
- 设Ax=b,其中A为非奇异阵。 (a)
- 设xi(i=0,1
- 写出求解方程组的Gauss-Seidel
- 已知a=1.2031,b=0.978是经
- 设L为单位下三角阵,试写出解方程组的算法
- 计算方法主要研究()误差和()误差。
- 用列主元消元法解线性方程组作第一次消元后
- 用二次拉格朗日插值多项式的值。插值节点和
- 求满足下列条件的埃尔米特插值多项式:
- 已知测量某长方形场地的长a=110米,宽
- 拉格朗日插值多项式的余项是()
- 设f(x)可微,求方程x=f(x)的牛顿
- 利用反幂法求矩阵的最接近于6的特征值及对
- 在某化学反应里,根据实验所得分解物的浓度
- 用高斯-塞德尔方法解方程组取,迭代四次(
- 设函数f(x)由下表给出: